## En demandant à la lib maths

Mon ordinateur m’indique que *π* vaut *approximativement*

    pi

    ## [1] 3.141593

## En utilisant la méthode des aiguilles du Buffon

Mais calculé avec la méthode des `aiguilles du Buffon`, on obtiendrait
comme **approximation** :

    set.seed(42)
    N = 100000
    x = runif(N)
    theta = pi/2*runif(N)
    2/(mean(x+sin(theta)>1))

    ## [1] 3.14327

## Avec un argument “fréquentiel” de surface

Sinon, une méthode plus simple à comprendre et ne faisant pas intervenir
d’appel à la fonction sinus se base sur le fait que si *X* ∼ *U*(0,1) et
*Y* ∼ *U*(0,1) alors *P*\[*X*<sup>2</sup>+*Y*<sup>2</sup>≤1\] = *π*/4
(voir [méthode de Monte Carlo sur
Wikipedia](https://fr.wikipedia.org/wiki/M%C3%A9thode_de_Monte-Carlo#D%C3%A9termination_de_la_valeur_de_%CF%80)).
Le code suivant illustre ce fait :

    set.seed(42)
    N = 1000
    df = data.frame(X = runif(N), Y = runif(N))
    df$Accept = (df$X**2 + df$Y**2 <=1)
    library(ggplot2)
    ggplot(df, aes(x=X,y=Y,color=Accept)) + geom_point(alpha=.2) + coord_fixed() + theme_bw()

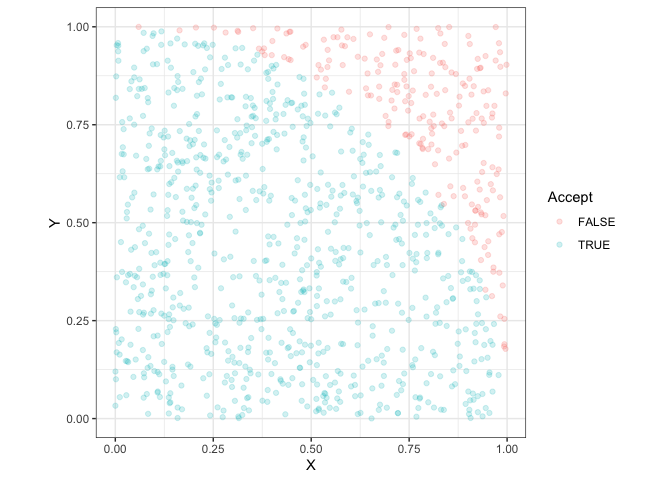![](module2-exo1_files/figure-markdown_strict/unnamed-chunk-3-1.png) Il
est alors aisé d’obtenir une approximation (pas terrible) de *π* en
comptant combien de fois, en moyenne, *X*<sup>2</sup> + *Y*<sup>2</sup>
est inférieur à 1 :

    4*mean(df$Accept)

    ## [1] 3.156