Quelques chiffres autour de l'épidémie de Covid-19
Table des matières
1 Identification du système
date "+%Y-%m-%d"
2020-06-01
uname -a
Linux silicium 5.4.0-33-generic #37-Ubuntu SMP Thu May 21 12:53:59 UTC 2020 x86_64 x86_64 x86_64 GNU/Linux
import sys
sys.version
3.8.2 (default, Apr 27 2020, 15:53:34) [GCC 9.3.0]
2 Récupération des données
On prend les données distribuées par Our World In Data, elles-mêmes issues de l'ECDC :
url = "https://covid.ourworldindata.org/data/ecdc/full_data.csv" data_raw = pd.read_csv(url, index_col='date') data_raw.tail(3)
location new_cases new_deaths total_cases total_deaths
date
2020-05-29 Zimbabwe 17 0 149 4
2020-05-30 Zimbabwe 11 0 160 4
2020-05-31 Zimbabwe 14 0 174 4
3 Evolution comparée de l'épidémie dans quelques pays
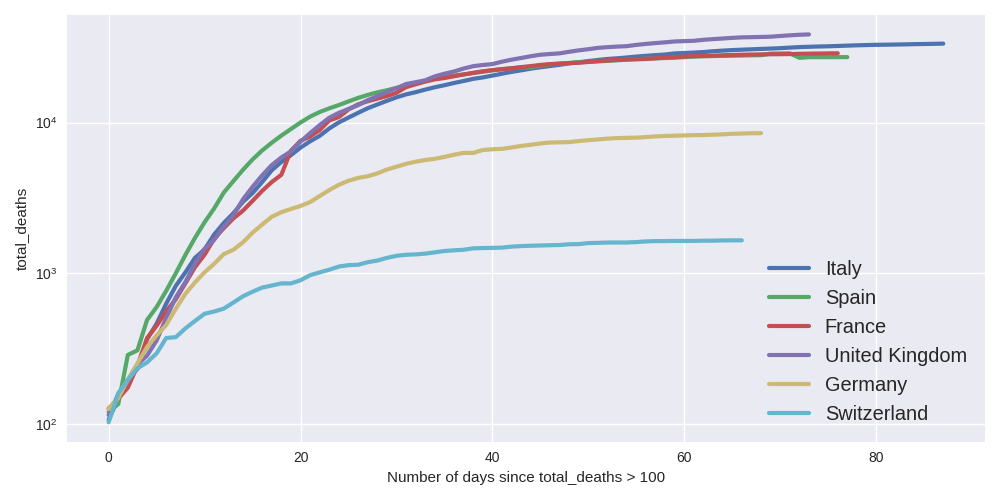
Je préfère fonder l'analyse sur le nombre de décès, qui me semble plus fiable et comparable d'un pays à l'autre que, par exemple, le nombre de cas dépistés. Afin de recaler l'axe temporel, on positionne \(t=0\) au moment où le nombre total de morts dépasse 100.
La logique est la suivante : on considère le nombre \(n^c\) (de décès ou de cas) dans un pays \(c\). On suppose que l'évolution de \(n^c\) en fonction du temps \(t\) suit une loi de croissance exponentielle (au moins dans une phase initiale). On s'attend ainsi à avoir une expression du type : \[ n^c(t) = n^c_0 \, e^{\lambda^c \left(t-t^c_0\right)}. \] Dans cette expression, la valeur initiale \(n^c_0 = n^c(t^c_0)\) est liée à la taille de la population considérée. La constante de temps \(\lambda^c\) en revanche, n'a pas vraiment de raison de l'être : elle reflète simplement le rythme auquel l'épidémie se propage.
Si l'on se donne un seuil \(\tau\) unique, on peut fixer pour chaque pays l'instant initial \(t^c_0\) de sorte que \[ n^c(t^c_0) = \tau. \] En effectuant un recalage de l'instant initial, c'est à dire en effectuant le changement de variable temporelle \(\tilde{t}^c=t-t^c_0\), on obtient \[ n^c(\tilde{t}^c) = \tau \, e^{\lambda^c\,\tilde{t}^c}, \] ce qui signifie que tous les pays deviennent comparables, indépendamment de leur taille : on s'est ramené à comparer les constantes de temps \(\lambda^c\) entre elles.
En pratique, on prend \[ t^c_0 = \min \left\{t ; n^c(t) > \tau \right\}. \]
# Parameters column = "total_deaths" threshold = 100 countries = ["Italy", "Spain", "France", "United Kingdom", "Germany", "Switzerland"] total = {} for country in countries: total[country] = data_raw.query(f"location == '{country}' & {column} > {threshold}") total[countries[2]]
location new_cases new_deaths total_cases total_deaths
date
2020-03-16 France 924 36 5423 127
2020-03-17 France 1210 21 6633 148
2020-03-18 France 1097 27 7730 175
2020-03-19 France 1404 69 9134 244
2020-03-20 France 1861 128 10995 372
... ... ... ... ... ...
2020-05-27 France 276 98 145555 28530
2020-05-28 France 191 66 145746 28596
2020-05-29 France 3325 66 149071 28662
2020-05-30 France 597 52 149668 28714
2020-05-31 France 1828 57 151496 28771
[77 rows x 5 columns]
4 Vers un passage du pic ?
On s'intéresse ici à l'atteinte d'un pic du nombre de décès quotidiens liés à Covid-19. Là encore, l'axe temporel est recalé afin de permettre une comparaison entre pays : \(t=0\) est positionné au moment où le nombre quotidien de morts dépasse 15.
threshold = 15 daily = {} for country in countries: daily[country] = data_raw.query(f"location == '{country}' & new_deaths > {threshold}") daily[countries[2]]
location new_cases new_deaths total_cases total_deaths
date
2020-03-14 France 785 18 3661 79
2020-03-16 France 924 36 5423 127
2020-03-17 France 1210 21 6633 148
2020-03-18 France 1097 27 7730 175
2020-03-19 France 1404 69 9134 244
... ... ... ... ... ...
2020-05-27 France 276 98 145555 28530
2020-05-28 France 191 66 145746 28596
2020-05-29 France 3325 66 149071 28662
2020-05-30 France 597 52 149668 28714
2020-05-31 France 1828 57 151496 28771
[78 rows x 5 columns]
Le pic observé pour la France au 04/04 (jour 20 sur le graphique) correspond à la prise en compte instantanée de tous les décès en EHPAD, dont le décompte est disponible à partir du 01/02 (cf. données du gouvernement)
