Analyse du risque de défaillance des joints toriques de la navette Challenger
Table des matières
Le 27 Janvier 1986, veille du décollage de la navette Challenger, eu lieu une télé-conférence de trois heures entre les ingénieurs de la Morton Thiokol (constructeur d'un des moteurs) et de la NASA. La discussion portait principalement sur les conséquences de la température prévue au moment du décollage de 31°F (juste en dessous de 0°C) sur le succès du vol et en particulier sur la performance des joints toriques utilisés dans les moteurs. En effet, aucun test n'avait été effectué à cette température.
L'étude qui suit reprend donc une partie des analyses effectuées cette nuit là et dont l'objectif était d'évaluer l'influence potentielle de la température et de la pression à laquelle sont soumis les joints toriques sur leur probabilité de dysfonctionnement. Pour cela, nous disposons des résultats des expériences réalisées par les ingénieurs de la NASA durant les 6 années précédant le lancement de la navette Challenger.
1. Chargement des données
Nous commençons donc par charger ces données:
import numpy as np import pandas as pd data = pd.read_csv("shuttle.csv") data
Date Count Temperature Pressure Malfunction
0 4/12/81 6 66 50 0
1 11/12/81 6 70 50 1
2 3/22/82 6 69 50 0
3 11/11/82 6 68 50 0
4 4/04/83 6 67 50 0
5 6/18/82 6 72 50 0
6 8/30/83 6 73 100 0
7 11/28/83 6 70 100 0
8 2/03/84 6 57 200 1
9 4/06/84 6 63 200 1
10 8/30/84 6 70 200 1
11 10/05/84 6 78 200 0
12 11/08/84 6 67 200 0
13 1/24/85 6 53 200 2
14 4/12/85 6 67 200 0
15 4/29/85 6 75 200 0
16 6/17/85 6 70 200 0
17 7/29/85 6 81 200 0
18 8/27/85 6 76 200 0
19 10/03/85 6 79 200 0
20 10/30/85 6 75 200 2
21 11/26/85 6 76 200 0
22 1/12/86 6 58 200 1
Le jeu de données nous indique la date de l'essai, le nombre de joints toriques mesurés (il y en a 6 sur le lançeur principal), la température (en Fahrenheit) et la pression (en psi), et enfin le nombre de dysfonctionnements relevés.
2. Inspection graphique des données
À première vue, ni l'information de pression ni la date nous apporteront des réponses sur la fréquence des incidents. On va donc chercher à filtrer les colonnes restantes en fusionnant les doublons pour la température.
agg_functions = {'Count': 'sum', 'Malfunction': 'sum'} data = data[['Temperature','Count','Malfunction']].groupby('Temperature', as_index=False).sum() data
Temperature Count Malfunction
0 53 6 2
1 57 6 1
2 58 6 1
3 63 6 1
4 66 6 0
5 67 18 0
6 68 6 0
7 69 6 0
8 70 24 2
9 72 6 0
10 73 6 0
11 75 12 2
12 76 12 0
13 78 6 0
14 79 6 0
15 81 6 0
Comment la fréquence d'échecs varie-t-elle avec la température ?
import matplotlib.pyplot as plt plt.clf() data["Frequency"]=data.Malfunction/data.Count data.plot(x="Temperature",y="Frequency",kind="scatter",ylim=[0,1]) plt.grid(True) plt.savefig(matplot_lib_filename) print(matplot_lib_filename)
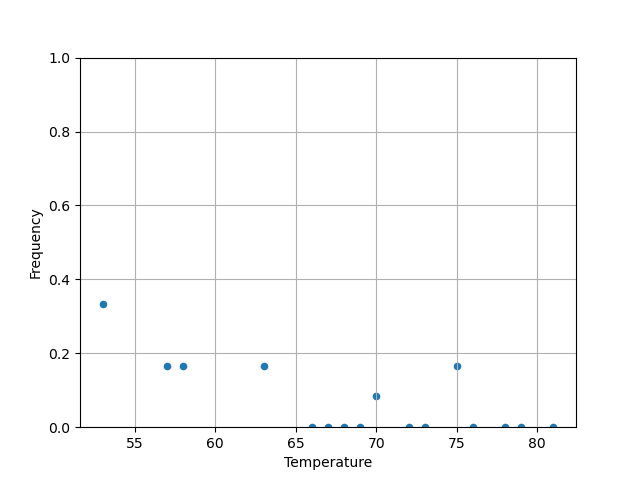
Contrairement à l'analyse précédente où les températures sans incidents n'étaient pas incluses, on voit ici une augemntation un peu plus nette de la fréquence des incidents à mesure que la température.
On peut procéder à une estimation de l'impact de la température \(t\) sur la probabilité de dysfonctionnements d'un joint.
3. Estimation de l'influence de la température
Supposons que chacun des 6 joints toriques est endommagé avec la même probabilité et indépendamment des autres et que cette probabilité ne dépend que de la température. Si on note \(p(t)\) cette probabilité, le nombre de joints \(D\) dysfonctionnant lorsque l'on effectue le vol à température \(t\) suit une loi binomiale de paramètre \(n=6\) et \(p=p(t)\). Pour relier \(p(t)\) à \(t\), on va donc effectuer une régression logistique.
import statsmodels.api as sm data["Success"]=data.Count-data.Malfunction data["Intercept"]=1 logmodel=sm.GLM(data['Frequency'], data[['Intercept','Temperature']], family=sm.families.Binomial(sm.families.links.logit())).fit() logmodel.summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: Frequency No. Observations: 16
Model: GLM Df Residuals: 14
Model Family: Binomial Df Model: 1
Link Function: logit Scale: 1.0000
Method: IRLS Log-Likelihood: -2.4880
Date: Tue, 11 Jun 2024 Deviance: 1.1965
Time: 16:14:26 Pearson chi2: 1.82
No. Iterations: 6 Pseudo R-squ. (CS): 0.07675
Covariance Type: nonrobust
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept 6.8667 8.822 0.778 0.436 -10.424 24.157
Temperature -0.1458 0.143 -1.023 0.306 -0.425 0.134
===============================================================================
L'estimateur le plus probable du paramètre de température est -0.1458 donc on peut s'attendre à une correlation négative entre la température et la propabilité de dysfonctionnement. L'erreur standard reste plutôt élevée mais le pseudo-R² reste bas, on peut avoir une certaine confiance en nos prédictions.
4. Estimation de la probabilité de dysfonctionnant des joints toriques
La température prévue le jour du décollage est de 31°F. Essayons d'estimer la probabilité de dysfonctionnement des joints toriques à cette température à partir du modèle que nous venons de construire:
import matplotlib.pyplot as plt data_pred = pd.DataFrame({'Temperature': np.linspace(start=30, stop=90, num=121), 'Intercept': 1}) data_pred['Frequency'] = logmodel.predict(data_pred[['Intercept','Temperature']]) data_pred.plot(x="Temperature",y="Frequency",kind="line",ylim=[0,1]) plt.scatter(x=data["Temperature"],y=data["Frequency"]) plt.grid(True) plt.savefig(matplot_lib_filename) print(matplot_lib_filename)

Contrairement à l'analyze précédente, on voit que la température a bien un effet considérable sur la probabilité de dysfonctionnement des joins toriques. Ainsi à 31°F, notre modèle prédit qu'un joint torique à plus de 90% de chances de dysfonctionner.
data_pred[data_pred.Temperature<=31.0]
Temperature Intercept Frequency 0 30.0 1 0.923566 1 30.5 1 0.918258 2 31.0 1 0.912615
La probabilité qu'un joint défaille à cette température est de \(p=0.913\). Sachant qu'il existe un joint primaire un joint secondaire sur chacune des trois parties du lançeur, la probabilité de défaillance des deux joints d'un lançeur est de \(p^2 \approx 0.833569\). La probabilité de défaillance d'un des lançeur est donc de \(1-(1-p^2)^3 \approx 99.5%\). La catastrophe était certaine.